
六、拆分法
数的拆分是解决一些分段数学问题的有效方法,一般可以把一个数拆分成几个数的和或者积的形式。可以根据数字的性质,尤其是整除特性和尾数规律,运用我们学过的运算定律,有目的地对数字进行快速拆分,以达到比采用常规的列方程、十字交叉和代入排除等方法省时省力的目的。数的拆分和转化可以将数量的间接联系转化为直接联系,进而能够利用已知条件进行直接的比较和计算。
例如,计算:
10634×4321+5317×1358
此题如果直接乘之后相加,数字较大,而且非常容易出错。如果将10634变为5317×2,规律就出现了。
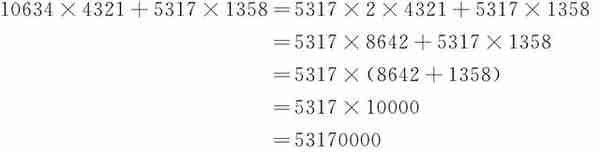
提取公因式是运用拆分法的典型例子。提取公因式进行简化计算是一个最基本的四则运算方法,但一定要注意提取公因式时公因式的选择。
例如,计算:
999999×777778+333333×666666
方法一:

方法二:

方法一和方法二在公因式的选择上有所不同,导致计算的简便程度不相同。
1.用拆分法算加法1
我们在做加法的时候,一般都是从右往左计算,这样方便进位。而在印度,他们都是从左往右算的。因为我们写数字的时候是从左往右写的,所以从左往右算会大大提高计算速度。这也是印度人计算速度比我们快的主要原因。从左到右计算加法就需要对数字进行拆分。
方法:
我们以第二个加数为三位数为例说明。
(1)先用第一个加数加上第二个加数的整百数。
(2)用上一步的结果加上第二个加数的整十数。
(3)用上一步的结果加上第二个加数的个位数即可。
例子:
(1)计算48+21= 。
解:
48+20=68
68+1=69
所以 48+21=69
(2)计算475+214= 。
解:
475+200=675
675+10=685
685+4=689
所以 475+214=689
(3)计算756+829= 。
解:
756+800=1556
1556+20=1576
1576+9=1585
所以 756+829=1585
注意:这种方法其实就是把第二个加数拆分成容易计算的数分别相加。
练习:
(1)计算489+223= 。
(2)计算1482+2211= 。
(3)计算1248+3221= 。
2.用拆分法算加法2
上面的方法中把一个加数进行了拆分,在本节中我们来学习如何把两个加数同时进行拆分。下面以三位数加法作为示例:如果两个加数都是三位数,那么可以把它们分别分解成百位、十位和个位三部分,然后分别进行计算,最后相加。
方法:
(1)把两个加数的百位数字相加。
(2)把两个加数的十位数字相加。
(3)把两个加数的个位数字相加。
(4)把前三步的结果相加,注意进位。
口诀:百加百,十加十,个加个。
例子:
(1)计算328+321= 。
解:
300+300=600
20+20=40
8+1=9
600+40+9=649
所以 328+321=649
(2)计算175+242= 。
解:
100+200=300
70+40=110
5+2=7
300+110+7=417
所以 175+242=417
(3)计算538+289= 。
解:
500+200=700
30+80=110
8+9=17
700+110+17=827
所以 538+289=827
注意:这种方法还可以做多位数加多位数,而且并不一定需要两个加数的位数相同。
练习:
(1)计算132+926= 。
(2)计算4127+363= 。
(3)计算55212+2129= 。
3.用拆分法算减法
我们做减法的时候,也和做加法一样,一般都是从右往左计算,这样方便借位。而在印度,他们都是从左往右算的。同样,从左往右算减法也要用到拆分。
方法:
我们以减数为三位数为例说明。
(1)先用被减数减去减数的整百数。
(2)用上一步的结果减去减数的整十数。
(3)用上一步的结果减去减数的个位数即可。
例子:
(1)计算458-214= 。
解:
458-200=258
258-10=248
248-4=244
所以 458-214=244
(2)计算88-21= 。
解:
88-20=68
68-1=67
所以 88-21=67
(3)计算9125-1186= 。
解:
9125-1000=8125
8125-100=8025
8025-80=7945
7945-6=7939
所以 9125-1186=7939
注意:这种方法其实就是把减数分解成容易计算的数进行计算。
练习:
(1)计算2648-214= 。
(2)计算5128-1154= 。
(3)计算43958-12614= 。
4.被减数为100、1000、10000的减法
方法:
(1)把被减数写成x+10的形式。例如100写成90+10,1000写成990+10,等等。
(2)用前面的数去减减数的十位以上数字,用10去减减数的个位数。可以避免借位。
例子:
(1)计算100-36= 。
解:
首先将被减数100写成90+10。
9-3=6
10-6=4
所以 100-36=64
(2)计算1000-316= 。
解:
首先将被减数1000写成990+10。
99-31=68
10-6=4
所以 1000-316=684
(3)计算10000-3365= 。
解:
首先将被减数10000写成9990+10。
999-336=663
10-5=5
所以 10000-3365=6635
注意:这种方法可以避免借位,提高准确率和计算速度。
练习:
(1)计算10000-2104= 。
(2)计算1000-24= 。
(3)计算100-21= 。
5.两位数减一位数
如果被减数是两位数,减数是一位数,那我们也可以把它们分别拆分成十位和个位两部分,然后分别进行计算,最后相加。
方法:
(1)把被减数分解成十位加个位的形式,把减数分解成10减去一个数字的形式。
(2)把两个十位数字相减。
(3)把两个个位数字相减。
(4)把上两步的结果相加,注意进位。
例子:
(1)计算22-8= 。
解:
首先把被减数分解成20+2的形式,减数分解成10-2的形式。
计算十位: 20-10=10
再计算个位: 2-(-2)=4
结果就是: 10+4=14
所以 22-8=14
(2)计算75-4= 。
解:
75=70+5, 4=10-6
70-10=60
5-(-6)=11
60+11=71
所以 75-4=71
(3)计算88-9= 。
解:
88=80+8, 9=10-1
80-10=70
8-(-1)=9
70+9=79
所以 88-9=79
练习:
(1)计算42-8= 。
(2)计算63-8= 。
(3)计算32-9= 。
6.两位数减法运算
如果两个数都是两位数,那么可以把它们分别拆分成十位和个位两部分,然后分别进行计算,最后相加。
方法:
(1)把被减数分解成十位加个位的形式,把减数分解成整十数减去一个数字的形式。
(2)把两个十位数字相减。
(3)把两个个位数字相减。
(4)把上两步的结果相加,注意进位。
例子:
(1)计算62-38= 。
解:
首先把被减数分解成60+2的形式,减数分解成40-2的形式。
计算十位: 60-40=20
再计算个位:2-(-2)=4
结果就是: 20+4=24
所以 62-38=24
(2)计算75-24= 。
解:
75=70+5, 24=30-6
70-30=40
5-(-6)=11
40+11=51
所以 75-24=51
(3)计算96-29= 。
解:
96=90+6, 29=30-1
90-30=60
6-(-1)=7
60+7=67
所以 96-29=67
练习:
(1)计算58-14= 。
(2)计算45-21= 。
(3)计算94-56= 。
7.三位数减两位数
方法:
(1)把被减数分解成百位加上一个数的形式,把减数拆分成整十数减去一个数字的形式。
(2)用被减数的百位与减数的整十数相减。
(3)用被减数的剩余数字与减数所减的数字相加。
(4)把上两步的结果相加,注意进位。
例子:
(1)计算212-28= 。
解:
首先把被减数分解成200+12的形式,减数分解成30-2的形式。
计算百位与整十数的差: 200-30=170
再计算剩余数字与所减数字的和: 12+2=14
结果就是: 170+14=184
所以 212-28=184
(2)计算105-84= 。
解:
105=100+5, 84=90-6
100-90=10
5+6=11
10+11=21
所以 105-84=21
(3)计算925-86= 。
解:
925=900+25, 86=90-4
900-90=810
25+4=29
810+29=839
所以 925-86=839
练习:
(1)计算458-14= 。
(2)计算124-47= 。
(3)计算528-89= 。
8.三位数减法运算
方法:
(1)把被减数分解成百位加上一个数的形式,把减数拆分成百位加上整十数减去一个数字的形式。
(2)用被减数的百位减去减数的百位,再减去整十数。
(3)用被减数的剩余数字与减数所减的数字相加。
(4)把上两步的结果相加,注意进位。
例子:
(1)计算512-128= 。
解:
首先把被减数分解成500+12的形式,减数分解成100+30-2的形式。
计算百位与百位和整十数的差:500-100-30=370
再计算剩余数字与所减数字的和:12+2=14
结果就是:370+14=384
所以 512-128=384
(2)计算806-174= 。
解:
806=800+6, 174=100+80-6
800-100-80=620
6+6=12
620+12=632
所以 806-174=632
(3)计算916-573= 。
解:
916=900+16, 573=500+80-7
900-500-80=320
16+7=23
320+23=343
所以 916-573=343
练习:
(1)计算528-157= 。
(2)计算469-418= 。
(3)计算694-491= 。
9.用拆分法算两位数乘法
我们知道一个两位数或者三位数乘以一位数比两位数乘以两位数要更容易计算,所以,两位数乘法中,如果被乘数或者乘数可以分解成两个一位数的乘积,那么可以把两位数乘法转换成一个两位数或者三位数乘以一位数的问题来简化计算。
方法:
(1)把其中一个两位数分解成两个一位数的乘积。
(2)用另外一个两位数与第一个一位数相乘。
(3)用上一步的结果(可能是两位数也可能是三位数)与第二个一位数相乘。
例子:
(1)计算51×24= 。
解:
24=4×6
51×4=204
204×6=1224
所以51×24=1224当然,本题也可以把24拆分成3×8。
24=3×8
解:
51×3=153
153×8=1224
所以 51×24=1224
(2)计算81×94= 。
解:
81=9×9
9×94=846
9×846=7614
所以 81×94=7614
(3)计算78×63= 。
解:
63=7×9
78×7=546
546×9=4914
所以 78×63=4914
注意:本方法可以扩展成多位数与两位数相乘。
练习:
(1)计算72×19= 。
(2)计算94×35= 。
(3)计算59×27= 。
10.将数字分解成容易计算的数字
有的时候,我们还可以把被乘数和乘数都进行拆分,使它变为容易计算的数字进行计算。这个时候要充分利用5、25、50、100等数字在计算时的简便性。
例子:
(1)计算48×27= 。
解:
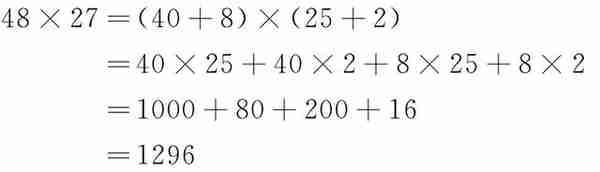
所以 48×27=1296
(2)计算62×51= 。
解:
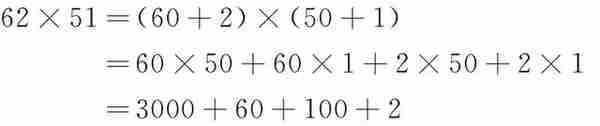
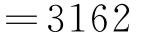
所以 62×51=3162
(3)计算84×127= 。
解:
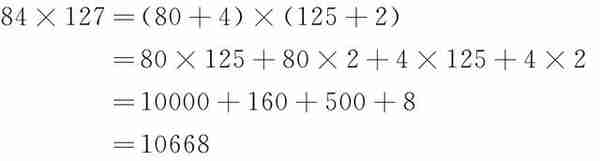
所以 84×127=10668
练习:
(1)计算127×88= 。
(2)计算192×55= 。
(3)计算98×52= 。
11.任意数字与12相乘
方法:
(1)将这个数字扩大10倍。
(2)求出这个数字的倍数。
(3)把前两步的结果相加。
例子:
(1)计算15×12= 。
解:
15扩大10倍为150,
15的倍数为30。
150+30=180
所以 15×12=180
(2)计算99×12= 。
解:
99扩大10倍为990,
99的倍数为198。
990+198=1188
所以 99×12=1188
(3)计算158×12= 。
解:
158扩大10倍为1580,
158的倍数为316。
1580+316=1896
所以 158×12=1896
注意:本题的方法可以扩展到多种情况,例如任意数字与11、13、15、21、22等相乘。因为一个任意数字乘以1、2、5等的计算都非常简单直观,所以将它们拆分成十位和个位分别计算可以大大降低计算难度。
练习:
(1)计算121×12= 。
(2)计算814×12= 。
(3)计算2259×22= 。
12.两位数与一位数相乘
方法:
(1)把这个两位数拆分成整十数和一个个位数(或者补数)。
(2)用这个整十数与一位数相乘。
(3)用个位数与一位数相乘。
(4)把前面两步的结果相加。
例子:
(1)计算51×8= 。
解:
51=50+1
50×8=400
1×8=8
400+8=408
所以 51×8=408
(2)计算99×7= 。
解:
99=90+9
90×7=630
9×7=63
630+63=693
所以 99×7=693
当然,本题也可以把99拆分成100-1。
99=100-1
解:
100×7=700
1×7=7
700-7=693
所以 99×7=693
(3)计算78×6= 。
解:
78=70+8
70×6=420
8×6=48
420+48=468
所以 78×6=468
注意:本方法可以扩展成多位数与一位数相乘。
练习:
(1)计算81×9= 。
(2)计算94×8= 。
(3)计算59×7= 。
13.两位数与两位数相乘
方法:
(1)把其中一个两位数拆分成整十数和一个个位数(或者补数)。
(2)用这个整十数与另一个两位数相乘。
(3)用这个个位数与另一个两位数相乘。
(4)把前面两步的结果相加。
例子:
(1)计算51×85= 。
解:
51=50+1
50×85=4250
1×85=85
4250+85=4335
所以 51×85=4335
(2)计算99×24= 。
解:
解法一
99=90+9
90×24=2160
9×24=216
2160+216=2376
所以 99×24=2376
解法二
当然,本题也可以把99拆分成100-1。
99=100-1
解:
100×24=2400
1×24=24
2400-24=2376
所以 99×24=2376
(3)计算78×63= 。
解:
78=70+8
70×63=4410
8×63=504
4410+504=4914
所以 78×63=4914
注意:本方法可以扩展成多位数与两位数相乘。
练习:
(1)计算81×19= 。
(2)计算94×82= 。
(3)计算59×27= 。
14.任意三位数的平方
我们可以把三位数拆分成一个一位数和一个两位数,再运用两位数的乘方方法来计算。
方法:
(1)用a×100+b来表示要计算平方的数,其中a为整百的数,b为十位和个位上的数。
(2)结果为(100a)2+2×100a×b+b2。
或者
(1)用a×10+b来表示要计算平方的数,其中a为整十的数,b为个位上的数。
(2)结果为(10a)2+2×10a×b+b2。
注意:要选择哪种拆分方法,应根据怎么拆平方更好算来确定。
例子:
(1)计算9152= 。
解:
9002=810000
2×900×15=27000
152=225
结果为: 810000+27000+225=837225
或
9102=828100
2×910×5=9100
52=25
结果为: 828100+9100+25=837225
所以 9152=837225
(2)计算5122= 。
解:
5002=250000
2×500×12=12000
122=144
结果为:250000+12000+144=262144
所以 5122=262144
(3)计算1292= 。
解:
1202=14400
2×120×9=2160
92=81
结果为: 14400+2160+81=16641
所以 1292=16641
练习:
(1)计算1192= 。
(2)计算2212= 。
(3)计算8152= 。
15.任意四位数的平方
我们把四位数拆分成两个两位数,运用两位数的乘方方法来计算。
方法:
(1)用a×100+b来表示要计算平方的数,其中a为整百的数,b为十位和个位上的数。
(2)结果为(100a)2+2×100a×b+b2。
例子:
(1)计算11132= 。
解:
11002=1210000
2×1100×13=28600
132=169
结果为: 1210000+28600+169=1238769
所以 11132=1238769
(2)计算15122= 。
解:
15002=2250000
2×1500×12=36000
122=144
结果为: 2250000+36000+144=2286144
所以 15122=2286144
(3)计算25112= 。
解:
25002=6250000
2×2500×11=55000
112=121
结果为: 6250000+55000+121=6305121
所以 25112=6305121
练习:
(1)计算11292= 。
(2)计算22172= 。
(3)计算15132= 。
16.任意数字与4相除
方法:
(1)先将除数除以2。
(2)再将上一步结果除以2。
例子:
(1)计算54÷4= 。
解:
将被除数除以2
得到 54÷2=27
再除以2
得到 27÷2=13.5
所以 54÷4=13.5
(2)计算108÷4= 。
解:
将被除数除以2
得到 108÷2=54
再除以2
得到 54÷2=27
所以 108÷4=27
(3)计算252÷4= 。
解:
将被除数除以2
得到 252÷2=126
再除以2
得到 126÷2=63
所以 252÷4=63
练习:
(1)计算1024÷4= 。
(2)计算56÷4= 。
(3)计算111÷4= 。
17.用拆分法算分数
方法:
把带分数拆分成整数和分数两部分进行计算。
例子:
(1)计算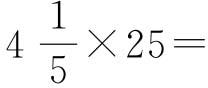 。
。
解:

所以 
(2)计算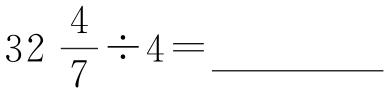 。
。
解:
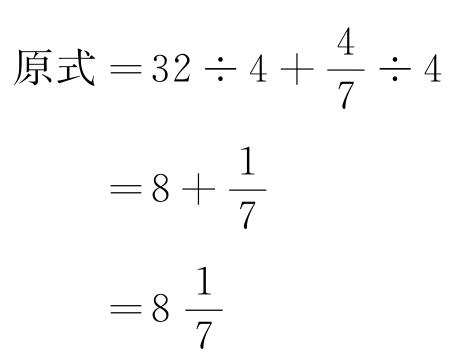
所以 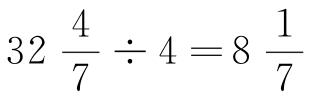
(3)计算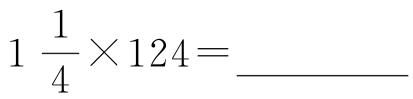 。
。
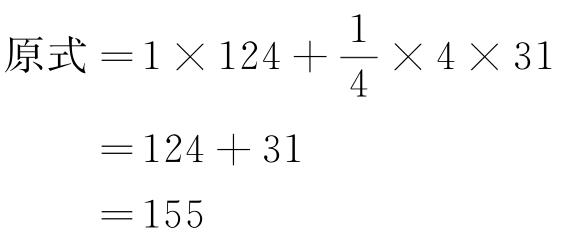
所以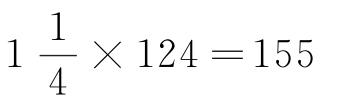
练习:
(1)计算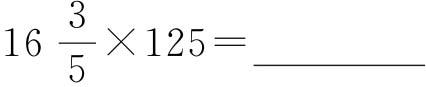 。
。
(2)计算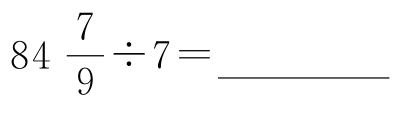 。
。
(3)计算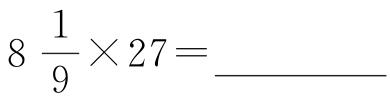 。
。
18.用裂项法算分数
裂项法也是拆分法的一种,该方法是将每个分数都分解成两个分数之差,并且使中间的分数相互抵消,从而简化运算。
方法:
裂项公式
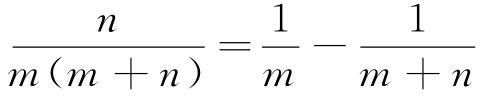
变化1
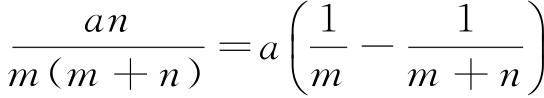
变化2
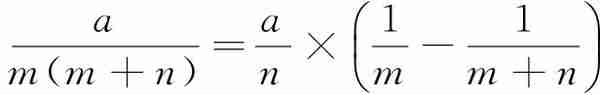
例子:
(1)计算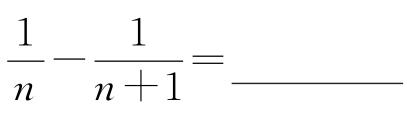 。
。
解:
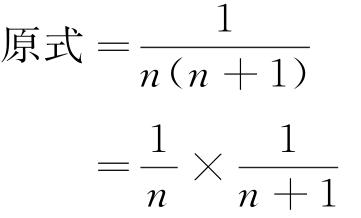
所以 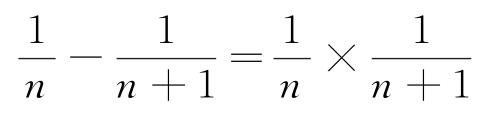
由这道题的规律我们可以看出,当分子都是1,分母是连续的两个自然数时,这两个分数的差就是这两个分数的积,反过来也同样成立,即这两个分数的积等于这两个分数的差。
根据这一关系,也可以简化运算过程。
(2)计算 。
。
解:
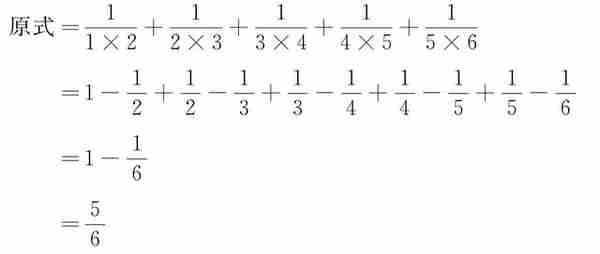
所以 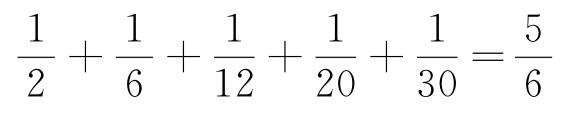
(3)计算数列an=n(n+1)的前n项和。
解:
an=n(n+1)=[n(n+1)(n+2)-(n-1)n(n+1)]/3(裂项)
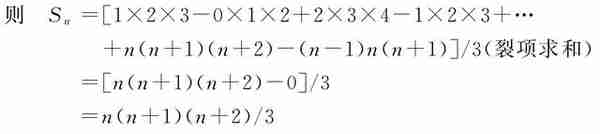
练习:
(1)计算 。
。
(2)计算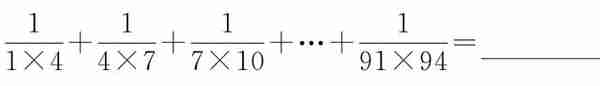 。
。
(3)计算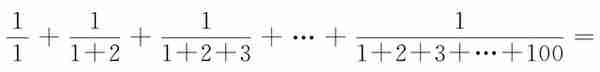 。
。